Функции сортировки и селекции
Сортировка и селекция выражений широко используются в практике символьных преобразований. Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм:
sort(L) sort(L. F) sort(A) sort(A. V)
Здесь L — список сортируемых значений, F — необязательная булева процедура с двумя аргументами, А — алгебраическое выражение, V — необязательные дополнительные переменные.

ПРИМЕЧАНИЕ
Вы можете проверить, что функция sort в Maple 7 способна сортировать буквы и даже слова русского языка.
Если функция сортировки меняет порядок расположения членов в выражении (или порядок расположения выражений), то другая функция — select — служит для выделения требуемого выражения:
select(f, e)
select(f, е. Ы. ..., bn)
Как бы обратной ей по действию служит функция remove, устраняющая заданные выражения:
remove(f, e)
remove(f, е, b1.... bn)
В этих функциях f — процедура, возвращающая логическое значение, е — список, множество, сумма, произведение или функция, b1, ..., bn — необязательные дополнительные аргументы.
Далее даны примеры применения этих функций.
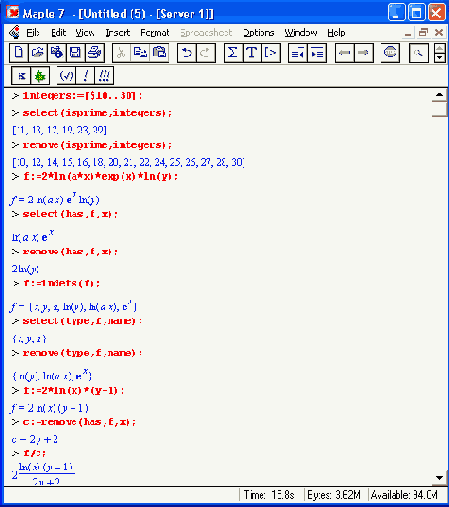
Maple имеет также оператор селекции А[ехрr]. Его действие поясняют следующие примеры:
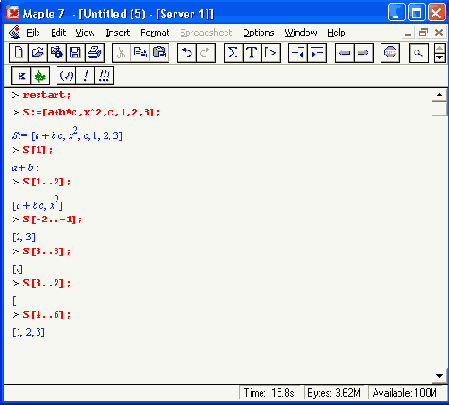

Функциональные преобразования элементов списков
Еще две функции, реализующие операции подстановки, указаны ниже:
map(fcn, expr. arg2. .... argn)
map2(fcn, argl, expr. arg3, .... argn)
Здесь fen — процедура или имя, expr — любое выражение, argi — необязательные дополнительные аргументы для fen.
Первая из этих функций позволяет приложить fen к операндам выражения ехрr. Приведенные далее примеры иллюстрируют использование функции mар.
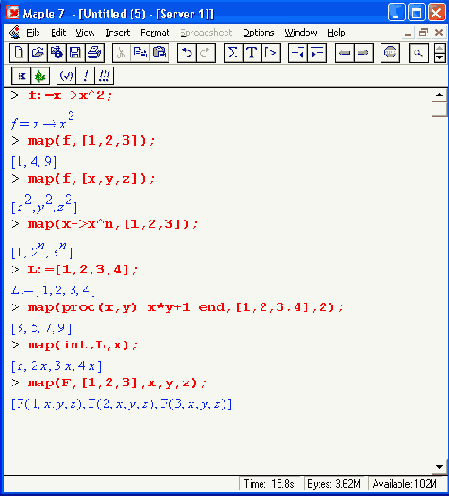
Из этих примеров нетрудно заметить, что если второй параметр функции mар — список, то функция (первый параметр) прикладывается к каждому элементу списка, так что возвращается также список. Из последнего примера видно, что если за вторым параметром идет перечисление аргументов, то они включаются в список параметров функции.
Функция mар2 отличается иным расположением параметров. Ее действие наглядно поясняют следующие примеры:
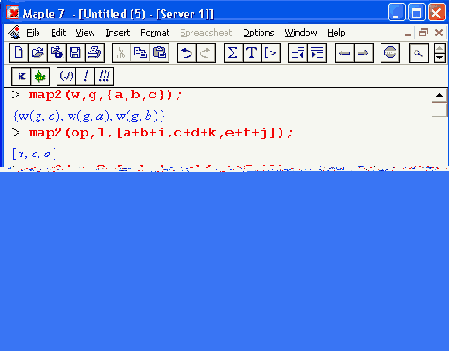
Функциональные преобразования подвыражений
Нередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения. Для этого можно воснользоваться функцией applyop:
applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е applyop(f, i, е. ..., xk, ...) — применяет функцию f к i'-му подвыражении выражения е с передачей необязательных дополнительных аргументов xk.Ниже даны примеры применения этой функции:
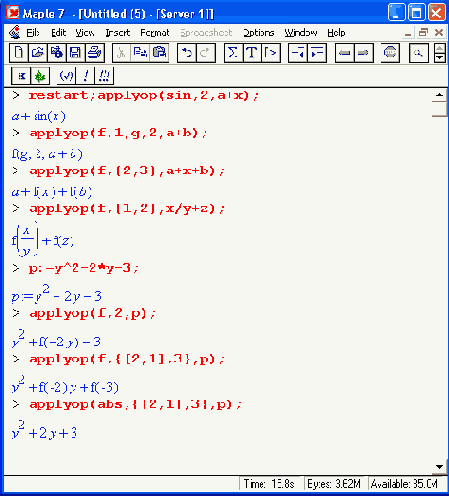
Комплектование по степеням
Еще одна функция общего назначения — collect — служит для комплектования выражения ехрr по степеням указанного фрагмента х (в том числе множества либо списка). Она задается в одной из следующих форм:
collect(a. x)
collect(a. x. form, func)
Во второй форме этой функции дополнительно задаются параметры form (форма) и func (функция или процедура). Параметр form может иметь два значения- recursive (рекурсивная форма) и distributed (дистрибутивная форма). Параметр func позволяет задать имя функции, по которой будет идти комплектование ехрr. Примеры применения функции collect представлены ниже:


Контроль за типами объектов
Выражения и их части в Maple 7 рассматриваются как объекты. В ходе манипуляций с ними важное значение имеет контроль за типом объектов. Одной из основных функций, обеспечивающих такой контроль, является функция whattype(object), возвращающая тип объекта, например string, integer, float, fraction, function и т. д. Могут также возвращаться данные об операторах. Примеры применения этой функции даны ниже:
> whattype(2+3);
integer
> whattype(Pi):
symbol
> whattype(123./5)
float
> whattype(l/3i:
fraction
> whattype(sin(x));
function
> whattype([1.2.3,a,b,c])
;list
> whattype(a+b+c);
+
> whattype(a*b/c):
*
> whattype(a'b):
^
> whattype(H-2+3=4);
=
С помощью функции type(object.t) можно выяснить, относится ли указанный объект к соответствующему типу t, например:
> type(2+3,integer):
true
> type(s1n(x).function);
true
> typeChello,string);
false
> type("hello",string);
true
> typed/3.fraction):
true
При успешном соответствии типа объекта указанному (второй параметр) функция type возвращает логическое значение true, в противном случае — false.
Для более детального анализа объектов может использоваться функция hastype(expr. t), где ехрr — любое выражение и t — наименование типа подобъекта.
Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении ехрr. Примеры применения этой функции даны ниже:
> hastype(2+3,integer);
true
> hastype(2+3/4.integer):
false
> hastype(2*sin(x).function);
true
> hastype(a+b-c/d,'+'):
true
Еще одна функция — has(f.x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае:
> has(2*sin(x),2);
true
> has(2*sin(x).V);
false
> has(2*sin(x),3-l);
true
Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3 - 1», если понимать его буквально, в выражении 2*sin(r) не содержится, но Maple-язык учитывает соответствие 3 - 1 = 2, и потому функция has в последнем примере возвращает true.
Подстановки с помощью функций add, mul и seq
Заметим, что операции, подобные описанным выше, Maple 7 реализует и с рядом других функций. Ограничимся примерами на подстановки с помощью функций сложения add, умножения mul и создания последовательностей seq:
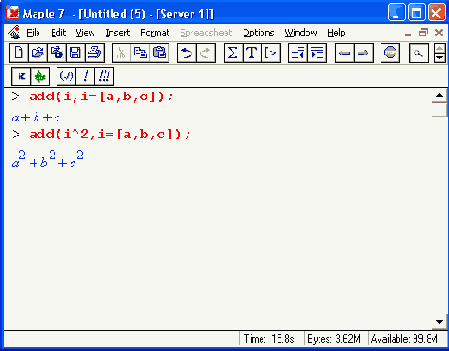

Подстановки с помощью функций subs и subsop
Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции: .,
subs(x=a.e) — в выражении е заменяет подвыражение х на подвыражение а; subs(sl,...,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков si, ..., sn вида х=а; subsop(eql, eq2, .... eqi, ...eqn, e) — в выражении е заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены.Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок:

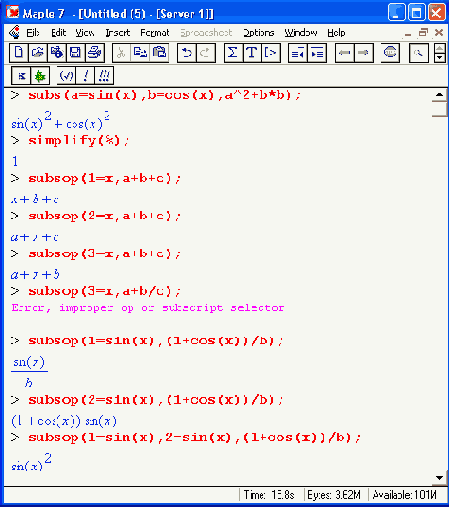
Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность.
Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:
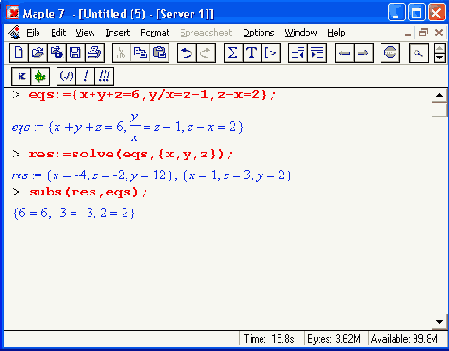
Здесь задана система из трех нелинейных уравнений, которая затем решена функцией solve. В конце примера с помощью функции подстановки выполнена проверка правильности решения. Оно верно, поскольку у всех уравнений значение левой части совпадает со значением правой части.
Преобразование выражений
Еще одним мощным средством преобразования выражений является функция combine. Она обеспечивает объединение показателей степенных функций и преобразование тригонометрических и некоторых иных функций. Эта функция -может записываться в трех формах:
combine(f)
combinef(, n)
combine(f. n. optl. opt2. ...)
Здесь f — любое выражение, множество или список выражений; n — имя, список или множество имен; optl, opt2, ... — имена параметров. Во втором аргументе можно использовать следующие функции:
| @@ |
abs |
arctan |
conjugate |
exp |
| In |
piecewise |
polylog |
power |
product |
| Ps |
radical |
range |
signum |
trig |
Примеры применения функции combine представлены ниже:
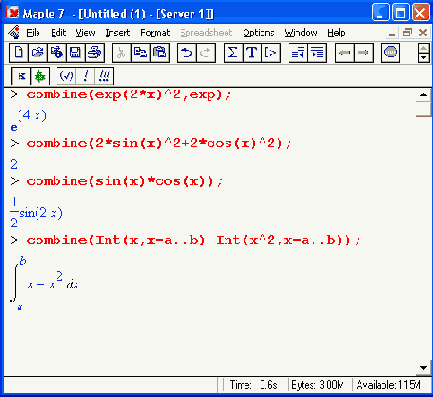
Эти примеры далеко не исчерпывают возможностей функции combine в преобразовании выражений. Рекомендуется обзорно просмотреть примеры применения функции combine с разными параметрами, приведенные в справочной системе Maple 7.
Преобразование выражений в тождественные формы
Многие математические выражения имеют различные тождественные формы. Порою преобразование выражения из одной формы в другую позволяет получить результат, более удобный для последующих вычислений. Кроме того, различные функции Maple 7 работают с разными формами выражений и разными типами данных. Поэтому большое значение имеет целенаправленное преобразование выражений и данных.
Основной функцией для такого преобразования является функция convert:
convert(expr. form, аrgЗ. ...)
Здесь ехрr — любое выражение, form — наименование формы, аrg3, ... — необязательные дополнительные аргументы.
convert — простая и вместе с тем очень мощная функция. Ее мощь заключается в возможности задания множества параметров. Их полный перечень (76 штук!) можно найти в справке по функции convert. Многие из этих параметров очевидны с первого взгляда, поскольку повторяют наименования типов чисел, данных или функций. Например, опции binary, decimal, hex и octal преобразуют заданные числа в их двоичное, десятичное, шестнадцатеричное и восьмеричное представление. Параметр vector задает преобразование списка в вектор (напоминаем, что список и вектор — разные типы данных), а параметр matrix — в матрицу. Приведем примеры применения функции convert:


Из этих примеров (их список читатель может пополнить самостоятельно) следует, что функция преобразования convert является одной из самых мощных функций Maple. С ее помощью можно получить множество различных форм одного и того же выражения.
Работа с частями выражений
Выражения (ехрr) или уравнения (eqn) обычно используются как сами по себе, так и в виде равенств или неравенств. В последнем случае объекты с выражениями имеют левую и правую части. Для простейших манипуляций с выражениями полезны следующие функции:
cost (а) — возвращает число сложений и умножений в выражении а (функция пакета codegen); Ihs(eqn) — выделяет левую часть eqn; rhs(eqn) — выделяет правую часть eqn; normal (ехрr) — дает нормализацию (сокращение) ехрr в виде дроби; numer(expr) — выделяет числитель ехрr; Оdenom(expr) — выделяет знаменатель ехрr.Ввиду очевидности действия этих функций ограничимся наглядными примерами их применения:

ПРИМЕЧАНИЕ
Обратите внимание на то, что в предшествующих версиях Maple загрузка библиотеч ной функции cost выполнялась иначе — командой readlib(cost). Это обстоятельство может служить причиной неверной работы документов, созданных в старых версиях Maple, в среде описываемой версии Maple 7.
 |
 |
Работа с уровнями вложенности выражений
В общем случае выражения могут быть многоуровневыми и содержать объекты, расположенные на разных уровнях вложенности. Приведем две функции для оценки уровней выражений и списков:
nops(expr) — возвращает число объектов первого уровня (операндов) в выражении ехрr; ор(ехрr) — возвращает список объектов первого уровня в выражении ехрr; ор(n.ехрr) — возвращает n-й объект первого уровня в выражении ехрr.Ниже представлены примеры применения этих функций:

Рекомендуется просмотреть и более сложные примеры на применение этих функций в справке.
Расширение выражений
Даже в жизни мы говорим: «не все так просто». Порою упрощенное выражение скрывает его особенности, знание которых является желательным. Функция expand «расширяет» выражение ехрr и записывается в виде:
expanc(expr, expr1, ехрг2, .... ехрrn)
где ехрr — расширяемое выражение, exprl, ехрг2, ..., ехрrn — необязательные подвыражения — опции. Имеется также инертная форма данной функции — Expand (ехрr). Кроме того, возможно применение операторной конструкции frontend(expans,[expr]).
Функция expand раскладывает рациональные выражения на простые дроби, полиномы на полиномиальные разложения, она способна раскрыть многие математические функции, такие как sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, In, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, Bessell, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE и функция piecewise. С помощью дополнительных аргументов expr1, ехрr2, ..., exprh можно задать расширение отдельных фрагментов в ехрr.
Примеры применения функции expand приведены ниже:

Разложение целых и рациональных чисел
Для разложения целых или рациональных чисел на множители в виде простых чисел служит функция:
ifactor(n)
или
ifactor(n,method)
где n — число, method — параметр, задающий метод разложения. Другая библиотечная функция, if actors(n), возвращает результат разложения в форме вложенных списков:

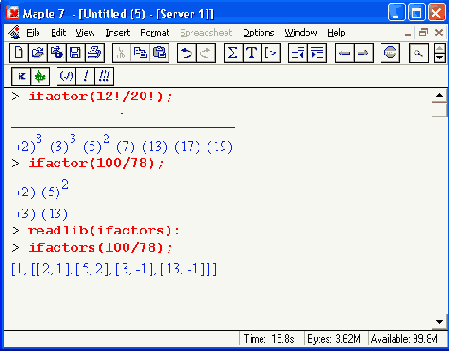
Разложение выражений (факторизация)
Для алгебраических выражений функция факторизации записывается в вычисляемой и не вычисляемой (инертной) формах:
factor(a) Factor(a)
factpr(a.K) Factor(а.К)
Здесь а — полином с несколькими переменными, К — необязательное алгебраическое расширение. Для получения результата от инертной формы функции факторизации надо использовать функции вычисления evala или evalgf.
Главная цель факторизации это нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы. Ниже представлены примеры применения функции factor:


Реализация итераций Ньютона в символьном виде
Найти достаточно простую и наглядную задачу, решение которой отсутствует в системе Maple 7, не очень просто. Поэтому для демонстрации решения задачи с применением аналитических методов воспользуемся примером, ставшим классическим, — реализуем итерационный метод Ньютона при решении нелинейного уравнения вида f(x) - 0.
Как известно, метод Ньютона сводится к итерационным вычислениям по следующей формуле:
xi+1=x1+f(x1)/f'(x1);
Реализующая его процедура выглядит довольно просто:
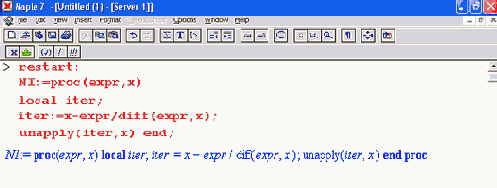
Для получения итерационной формулы в аналитическом виде здесь используется функция unapply. Теперь, если задать решаемое уравнение, то можно получить искомое аналитическое выражение:

Далее, задав начальное приближение для х в виде х = х0, можно получить результаты вычислений для ряда итераций:

Нетрудно заметить, что, испытав скачок в начале решения, значениях довольно быстро сходятся к конечному результату, дающему корень заданной функции. Последние три итерации дают одно и то же значение х. Заметим, что этот метод дает только одно решение, даже если корней несколько. Вычислить другие корни в таком случае можно, изменив начальное условие.
Можно попробовать с помощью полученной процедуры получить решение и для другой функции:

Здесь итерационная формула имеет (и вполне естественно) уже другой вид, но сходимость к корню также обеспечивается за несколько итераций. ;
Возможна и иная форма задания итерационной процедуры с применением оператора дифференцирования D и заданием исходной функции также в виде процедуры:
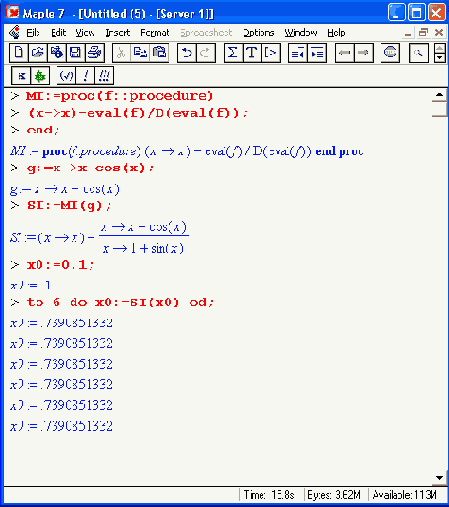
Вообще говоря, в программных процедурах можно использовать любые операторы и функции, присущие Maple-языку, в том числе и те, которые реализуют символьные вычисления. Это открывает широкий простор для разработки новых процедур и функций, обеспечивающих выполнение символьных операций.
Упрощение выражений
Функция simplify — одна из самых мощных в системах символьной математики. Она предназначена для упрощения математических выражений. «Все гениальное просто», — любим мы повторять, хотя это далеко не всегда так. Тем не менее стремление представить многие математические выражения в наиболее простом виде поощряется в большинстве вычислений и нередко составляет их цель. В системе Maple 7 функция упрощения используется в следующем виде:
simplify(expr) — возвращает упрощенное выражение ехрr или повторяет его, если упрощение в рамках правил Maple 7 невозможно; simplify(expr, nl, n2, ...) —возвращает упрощенное выражение ехрr с учетом параметров с именами nl, n2, ... (в том числе заданных списком или множеством); simplify(ехрг,assume=prop) — возвращает упрощенное выражение ехpr с учетом всех условий.Функция simplify — многоцелевая. Она обеспечивает упрощение математических выражений, выполняя следующие типовые действия (для простоты обозначим их как ->):
комбинируя цифровые подвыражения (3*х*5->15*х, 10*х/5->2*х); приводя подобные множители в произведениях (х^3*а*х->а*х^4); приводя подобные члены в суммах (5*х+2+3*х->8*х+2); используя тождества, содержащие ноль (а+0->а, х-0->х); используя тождества, содержащие единицу (1*х->х); распределяя целочисленные показатели степени в произведениях ((3*x*y^3)^2 ->9*х^2*у^6); сокращая ехрr на наибольший общий полиномиальный или иной множитель; понижая степень полиномов там, где это возможно; используя преобразования, способные упростить выражения.Несмотря на свою гибкость, функция simplify не всегда способна выполнить возможные упрощения. В этом случае ей надо подсказать, в какой области ищутся упрощения и где можно найти соответствующие упрощающие преобразования.
С этой целью в функцию simplify можно включать дополнительные параметры.
В качестве параметров могут задаваться имена специальных математических функций и указания на область действия упрощений: Bessell, BesselJ, BesselK, BesselY, Ei, GAMMA, RootOf, LambertW, dilog, exp, In, sqrt, polylog, pg, pochhammer, trig (для всех тригонометрических функций), hypergeom, radical, power и atsign (для операторов).
Полезен также параметр symbolic, явно указывающий на проведение символьных преобразований.
Возможно также применение функции simplify в форме simplify[<name>], где <name> — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, , sqrt, trig. Ниже даны примеры применения функции Simplifу:
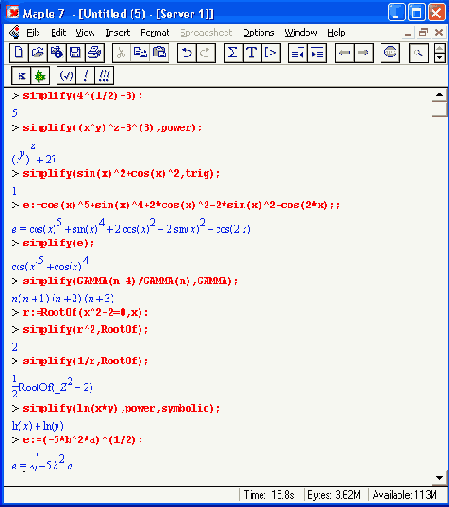

Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен:


 |
 |
 |
Вложенные процедуры и интегрирование по частям
Теперь мы подошли к важному моменту, о котором читатель наверняка уже давно догадался — в составляемых пользователем процедурах можно использовать ранее составленные им (или кем-то еще) другие процедуры! Таким образом, Maple-язык позволяет реализовать процедуры, вложенные друг в друга. Для иллюстрации применения вложенных процедур рассмотрим операцию интегрирования по частям. Пусть нам надо вычислить интеграл:

где р(х) — выражение, представляющее полином.
Приведенный ниже пример подготовлен в реализации Maple 7 [38]. Вначале подготовим процедуру IntExpMonomialR, реализующую вычисление уже рассмотренного ранее интеграла, но рекурсивным способом:
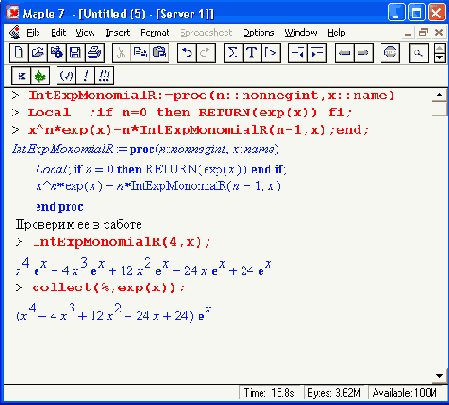
Теперь составим процедуру для вычисления по частям нашего интеграла:

В этой процедуре имеется обращение к ранее составленной процедуре IntExpMonomialR. Обратите внимание на то, что в процедуре введено предупреждение об определенных проблемах, связанных с использованием функции degree (сообщение начинается с символов ###). Тем не менее процедура работает, в чем убеждают по крайней мере следующие примеры:
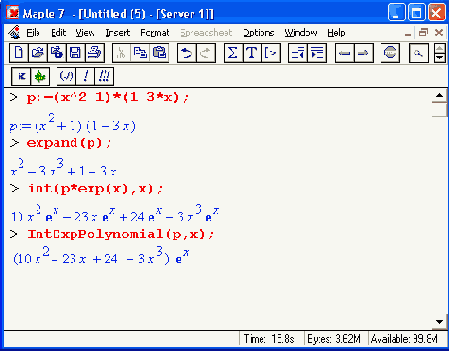
В заключение остается отметить, что данный пример в Maple V R4 дает неточный результат, хотя никаких сообщений об ошибках не выводится.
Вычисление интеграла по известной формуле
Рассмотрим следующий пример:
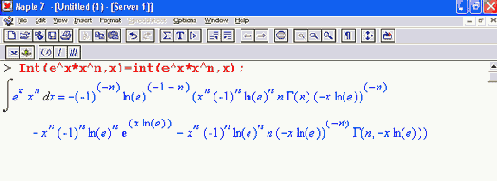
Прежние версии системы Maple не брали этот интеграл, поскольку он не имеет аналитического представления через обычные функции. Maple 7 блестяще вычисляет этот «крепкий орешек», но полученное выражение довольно сложно.
Из математики известно, что такой интеграл может быть представлен в следующем виде:
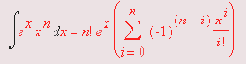
Используя эту формулу, мы можем создать простую процедуру для численного и аналитического вычисления данного интеграла:

Результат в аналитическом виде довольно прост для данного интеграла с конкретным значением т. Более того, мы получили несколько иной результат и дляп в общем случае. Но точен ли он? Для ответа на этот вопрос продифференцируем полученное выражение:
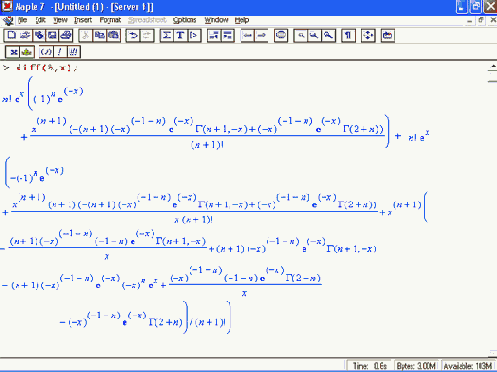
Результат дифференцирования выглядит куда сложнее, чем вычисленный интеграл. Однако с помощью функции simplify он упрощается к подынтегральной функции:
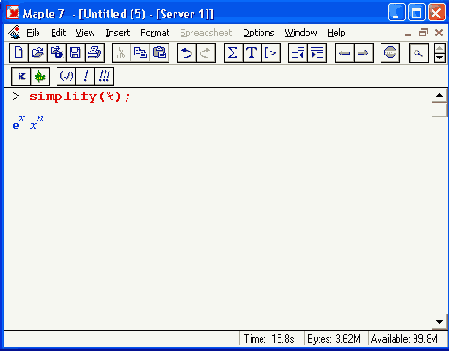
Это говорит о том, что задача вычисления заданного интеграла в аналитической форме действительно решена. А что касается громоздкости результатов, так ведь системы, подобные Maple 7, для того и созданы, чтобы облегчить нам работу с громоздкими вычислениями — в том числе аналитическими.
Глава 3D- графики параметрически заданных поверхностей
3d- графики параметрически заданных поверхностей
На рис. 11. 19 показано построение поверхности при полном ее параметрическом задании. В этом случае поверхность задается тремя формулами, содержащимися в списке.

В данном случае функциональная окраска задана из меню, поэтому в состав функции соответствующий параметр не введен. Обратите внимание на технику удаления частей фигуры путем задания соответствующего диапазона изменения параметров t и n.
Следующий пример показывает построение простого тороида — цилиндра, свернутого в кольцо (рис. 11.20). Здесь также использован прием удаления части фигуры, что делает ее представление более наглядным и красочным. Кроме того, введены параметры, задающие функциональную окраску.
Тор на рис. 11.20 выглядит, как произведение искусства. Он дает полное и наглядное представление об этой фигуре.
 |
 |
 |
Быстрое построение графиков
Двумерная быстрая графика — smartplot
В последние реализации системы Maple (5, 6 и 7) введены новые функции быстрого построения графиков. Функция smartplot(f) предназначена для создания двумерных графиков. Параметр f может задаваться в виде одиночного выражения или набора выражений, разделяемых запятыми. Задание управляющих парамтеров в этих графических функциях не предусмотрено; таким образом, их можно считать первичными, или черновыми. Для функции построения двумерного графика по умолчанию задан диапазон изменения аргумента -10.. 10. Рисунок 11.26 иллюстрирует применение функции smartplot для построения трех (верхний пример) и двух (нижний пример) графиков функций на одном рисунке.

а
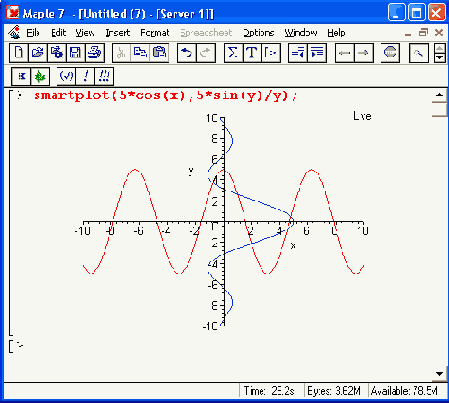
б
Рис. 11.26. Построение графиков с помощью функции smartplot
Обратите внимание на второй пример применения функции smartplot. Здесь график выражения 5sin(y)/y построен относительно вертикальной оси. Поэтому он развернут на 90° относительно графика, построенного обычным образом.
ПРИМЕЧАНИЕ
На графиках, построенных командой smartplot(x), присутствует надпись «Live», что — видно на рис. 11.26.
Быстрое построение трехмерных графиков smartplot3d
Быстрое построение трехмерных графиков smartplot3d
Быстрое (не в смысле ускорения самого построения, а лишь в смысле более быстрого задания построения графиков) построение трехмерных графиков обеспечивает функция smartplot3d Для этой функции задан диапазон изменения обоих аргументов -5..5. Рисунок 11.27 поясняет применение функции smartplot3d.

а

б
Рис. 11.27. Примеры применения функции smartplot3d
Как видно из второго примера, представленного на рис. 11.27, функция smartplot3d обеспечивает построение не только отдельных поверхностей, но и ряда Пересе, кающихся поверхностей. При этом линии пересечения поверхностей строятся вполне корректно.
 |
 |
 |
Двумерные и трехмерные графические структуры
Понятие о графических структурах
Функции PLOT и PLOT3D (с именами, набранными большими буквами) позволяют создавать графические структуры, содержащие ряд графических объектов si, s2, s3 и т. д. Каждый объект может представлять собой точку или фигуру, полигон, надпись и т. д., позиционированную с высокой точностью в заданной системе координат. Координатные оси также относятся к графическим объектам. Важно отметить, что функции PLOT и PLOT3D одновременно являются данными, описывающими графики. Их можно записывать в виде файлов и (после открытия файлов) представлять в виде графиков. Особые свойства этих функций подчеркиваются их записью прописными буквами.
Графические структуры двумерной графики
Графическая структура двумерной графики задается в виде:
PLOT(s1, s2, s3....,0);
где si, s2, s3 ... — графические объекты (или элементарные структуры — примитивы), о — общие для структуры параметры.
Основными объектами являются:
POINTS([xl,yl],[x2,y2],...[xn,yn]) — построение точек, заданных их координатами; CURVES([[xll,yll],...[xln,yln]], [[х21,у21],...[х2п,у2п]],... [[xml,yml]....[xmn.ymn]]) -построение кривых по точкам; POLYGONS([[xll,yll]....[xln,yln]], [x2l.y2ll]....[x21n,y21n]].... [[xml,yml]....[xmn.ynm]]) -построение замкнутой области-полигона (многоугольника, так как последняя точка должна совпадать с первой); ТЕХТ([х, у], 'string', horizontal .vertical) — вывод текстовой надписи 'string4, позиционированной в точке с координатами [х.у], с горизонтальной или вертикальной ориентацией. Параметр horizontal может иметь значение ALIGNLEFT или ALIGNRIGHT, указывающие, в какую сторону (влево или вправо) идет надпись. Аналогично параметр vertical может иметь значение ALIGNABOVE или ALIGNBELOW, указывающее в каком направлении (вверх или вниз) идет надпись.При задании графических объектов (структур) si, s2, s3 и т. д. можно использовать описанные выше параметры и параметры, например, для задания стиля построения - STYLE (POINT, LINE/PATCH, PATCHNOGRID); толщины линий, - THICKNESS (кроме координатных осей); символа, которым строятся точки кривых — SYMBOL (BOX, CROSS, CIRCLE, POINT, DIAMOND и DEFAULT); стиля линий - LINESTYLE; цвета -COLOR (например, COLOR(HUE.O) для закраски непрерывной области), типа шрифта — FONT; вывода титульной надписи — TITLE (string); имени объекта — NAME (string); стиля координатных осей - AXESSTYLE (BOX, FRAME, NORMAL, NONE или DEFAULT) и т. д.
Следует отметить, что параметры в графических структурах задаются несколько иначе — с помощью круглых скобок. Например, для задания шрифта TIMES ROMAN с размером символов 16 пунктов надо записать FONT(TIMES,ROMAN, 16), для задания стиля координатных осей в виде прямоугольника — AXESSTYLE (BOX) и т. д.
На рис. 11.31 показан пример графических построений при использовании основных структур двумерной графики.
Как видно из этого примера, графическая двумерная структура позволяет задавать практически любые двумерные графики и текстовые надписи в пределах одного рисунка.

Рис. 11.31. Пример использования двумерных структур
Графические структуры трехмерной графики
Графические структуры трехмерной графики
Графические структуры трехмерной графики строятся функцией PLOT3D:
PLOT3D(s1,s2,s3.....o)
В качестве элементарных графических структур можно использовать уже описанные выше объекты POINTS, CURVES, POLYGONS и TEXT — разумеется, с добавлением в списки параметров третьей координаты. Пример такого построения дан на рис. 11.32.
Кроме того, могут использоваться некоторые специальные трехмерные структуры. Одна из них — структура GRID:
GRID(a. .b,c..d.listlist) — задание поверхности над участком координатной плоскости, ограниченной отрезками[а, b] и[с, d], по данным, заданным переменной-списком listlist:=[[z11,...z1n],[z21,...z2n],...[z1m...zmn]] с размерностью n?m. Заметим, что эта переменная задает координату z для равноотстоящих точек поверхности. На рис. 11.33 показан пример создания структуры трехмерной графики на базе GRID. Изображение .представляет собой линии, соединяющие заданные точки.
Еще один тип трехмерной графической структуры — это MESH:
MESH(listlist) — задание трехмерной поверхности по данным списочной переменной list! 1st, содержащей полные координаты всех точек поверхности (возможно задание последней при неравномерной сетке).

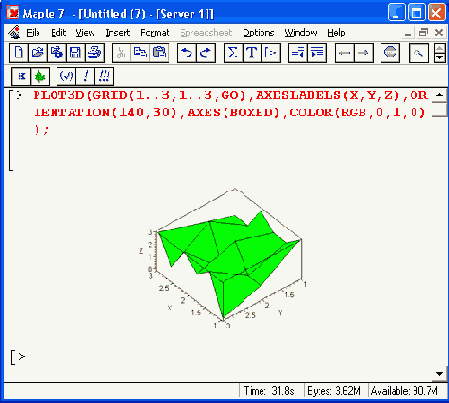
Обычная форма задания этой структуры следующая:
MESH([[[x11,y11,z11]....[x1n,y1n,z1n]]. [[x21,y21,z21]....[x2n,y2n,z2n]]. ...[[xm1,ym1,zm1]...[xmn,ymn,zmn]]])
Пример задания такой структуры представлен на рис. 11.34.
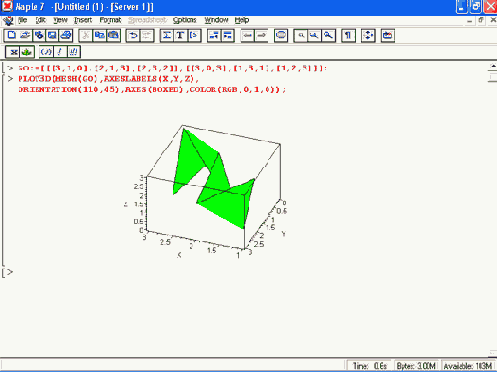
Описанные структуры могут использоваться и в программных модулях. Много таких примеров описано в книгах, поставляемых с системой Maple 7.
 |
 |
 |
Графики функций, построенные точками
Графики функций, построенные точками
Показанный на рис. 11. 5 график полинома, построенный ромбиками, не означает, что полином представлен отдельными точками. В данном случае просто выбран стиль линии в виде точек. Однако часто возникает необходимость построения графиков функций, которые представлены просто совокупностями точек. Такая совокупность может быть создана искусственно, как на рис. 11.7, либо просто задаваться списком координат х и значений функции.
В данном случае переменная Р имеет вид списка, в котором попарно перечислены координаты точек функции sin(x). В этом нетрудно убедиться, заменив знак «:» после выражения, задающего Р, на знак «;». Далее по списку Р построен график точек в виде крестиков, которые отображают отдельные значения функции sin(x).
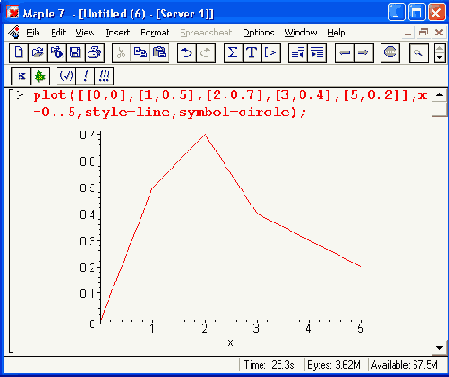
На рис. 11.8 показано построение графиков функций по точкам при явном задании функции списком координат ее отдельных точек. В первом примере эти точки соединяются отрезками прямых, так что получается кусочно-линейный график. Видно также, что указание типа точек после указания стиля линии игнорируется (а жаль, было бы неплохо, чтобы наряду с кусочно-линейной линией графика строились и выделенные окружностями точки).

а
б
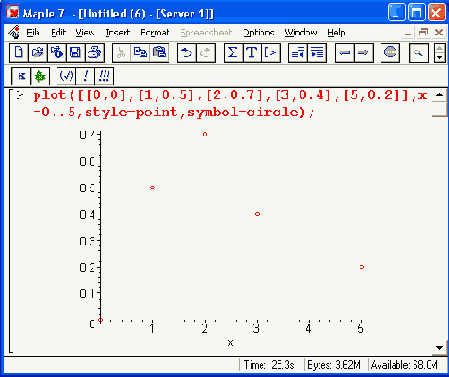
Рис. 11.8. Построение графика функции, явно заданной отдельными точками
Во втором примере рис. 11.8 показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками. Читателю предлагается самостоятельно совместить оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.
 |
 |
 |
Графики функций с ординатами, заданными вектором
Графики функций с ординатами, заданными вектором
Часто возникает необходимость построения графика точек, ординаты которых являются элементами некоторого вектора. Обычно при этом предполагается равномерное расположение точек по горизонтальной оси. Пример построения такого графика дан на рис. 11.10.
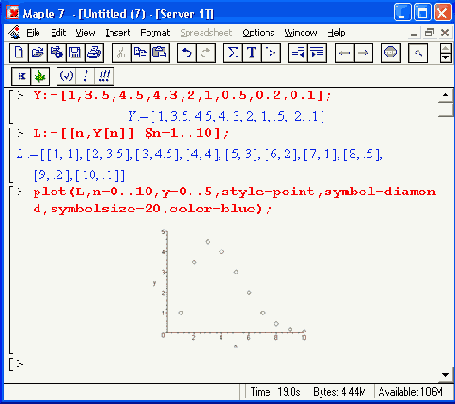
Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора, добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет, так что фактически строится график зависимости ординат точек от их порядкового номера n.
 |
 |
 |
Графики функций с разрывами
Некоторые функции, например tan(x), имеют при определенных значениях х разрывы, причем случается, что значения функции в этом месте устремляются в бесконечность. Функция tan(x), к примеру, в точках разрывов устремляется к +? и -?. Построение графиков таких функций нередко дает плохо предсказуемые результаты. Графический процессор Maple 7 не всегда в состоянии определить оптимальный диапазон по оси ординат, а график функции выглядит весьма непредставительно, если не сказать безобразно (рис. 11.3, первый пример).
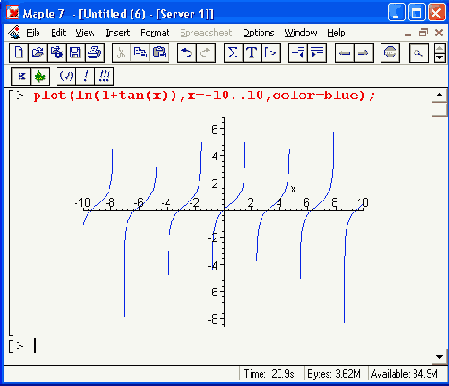
а

б
Рис. 11.3. Построение графиков функций с разрывами
Среди аргументов функции plot есть специальный параметр discont. Если задать его значение равным true, то качество графиков существенно улучшается, см. второй пример на рис. 11.3. Улучшение достигается разбиением графика на несколько участков, на которых функция непрерывна, и более тщательным контролем за отображаемым диапазоном. При discont=false данный параметр отключен и строятся обычные графики.
ПРИМЕЧАНИЕ
Следует отметить, что вид графика можно улучшить, просто задав диапазон по оси у например введя в параметры функции запись у=-10..10). При этом в точках разрыва могут появиться вертикальные линии. Иногда это бывает полезно.
Графики функций в неограниченном диапазоне
Изредка встречаются графики функций f(x), которые надо построить при изменении значениях от нуля до бесконечности или даже от минус бесконечности до плюс бесконечности. Бесконечность в таких случаях задается как особая константа infinity. В этом случае переменной х, устремляющейся в бесконечность, откладывается значение аrctan(x). Рисунок 11.2 (второй пример) иллюстрирует сказанное.
Графики функций в полярной системе координат
Графики функций в полярной системе координат
Графики в полярной системе координат представляют собой линии, которые описывают конец радиус- вектора r(t) при изменении угла t в определенных пределах — от t до t . Построение таких графиков также производится функцией plot, которая для этого записывается в следующем виде:

а

б
Рис. 11.13. Построение функций, заданных параметрически
plot([r(t),theta(t),t=tmin..tnrax],h,v,p,coords-polar)
Здесь существенным моментом является задание полярной системы координат параметром coords=polar. Рисунок 11.14 дает примеры построения графиков функций в полярной системе координат.
Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.
 |
 |
 |
Графики функций, заданных функциональными операторами
Графики функций, заданных функциональными операторами
Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется рис. 11.12.
Имена функций (без указания списка параметров в круглых скобках) тоже, по существу, являются функциональными операторами. Так что они также могут использоваться при построении графиков упрощенными способами.
Графики функций, заданных параметрически
Графики функций, заданных параметрически
В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например х = f1(t) и у =f2(t) при изменении переменной t в некоторых пределах. Точки(х, у) наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:
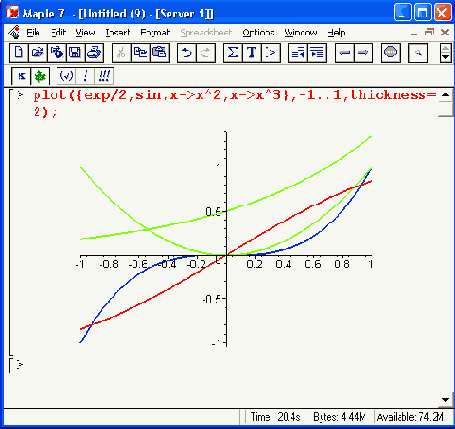
plot([fl(t),f2(t),t-tmin..tmax].h,v.p)
Если функции f1(£) и f2(0 содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0. .2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f1(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рисунок 11.13 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.
Задание диапазонов для изменений h и v, а также параметров р не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.
 |
 |
 |
Графики функций, заданных процедурами
Графики функций, заданных процедурами
Некоторые виды функций, например кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется рис. 11.11.


Рис. 11.11. Построение графика функций, заданных процедурами
Здесь, пожалуй, полезно обратить внимание на то, что в функции plot указывается имя процедуры без списка ее параметров.
 |
 |
 |
Графики функций, заданных своими именами
Графики функций, заданных своими именами
Способность Maple 7 к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения программы, на что уходят, увы, не дни, а месяцы, а то и годы. Применительно к графикам одной из таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках. Такую возможность наглядно демонстрирует рис. 11.9.

Этот пример показывает, что возможно построение графиков функций даже без указания в команде plot диапазонов. При этом диапазон по горизонтальной оси устанавливается равным по умолчанию -10.. 10, а по вертикальной оси выбирается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной (условно х).
 |
 |
 |
Графики нескольких функций на одном рисунке
Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае (рис. 11.4, первый пример) для построения таких графиков достаточно перечислить нужные функции и установить для них общие интервалы изменения.

Рис. 11.4. Графики трех функций на одном рисунке
Обычно графики разных функций автоматически строятся разными цветами. Но это не всегда удовлетворяет пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линий) и style (стиль линий), можно добиться выразительного выделения кривых — это показывает второй пример на рис. 11.4 для случая, когда линии графиков выделяются стилем. Однако если кривые задаются разным цветом, то при черно-белой печати они могут перестать различаться.
На рис. 11.5 показан еще один пример такого рода. Здесь построен график функции sin(x)/x и график ее полиномиальной аппроксимации. Она выполняется настолько просто, что соответствующие функции записаны прямо в списке параметров функции plot.

Рис. 11.5. График функции sin(x)/x и ее полиномиальной аппроксимации
В данном случае сама функция построена сплошной линией, а график полинома точками — ромбами. Хорошо видно, что при малых х аппроксимация дает высокую точность, но затем с ростом х ее погрешность резко возрастает.
Рисунок 11.6 показывает построение нескольких любопытных функций, полученных с помощью комбинаций элементарных функций. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.

Рис. 11.6. Построение графиков нескольких любопытных функций
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы.
Масштабирование трехмерных фигур и изменение углов их обзора
Масштабирование трехмерных фигур и изменение углов их обзора
Полезно обратить внимание на параметр масштаба scalling=constrained, явно введенный в документ рис. 11.20. Его можно было бы и не вводить, поскольку этот параметр задается по умолчанию. Он выравнивает масштабы представления фигуры по осям координат, обычно используется по умолчанию и позволяет снизить до минимума геометрические искажения фигур — тор, например, при этом виден как круглая труба, свернутая в кольцо. У таких графиков есть специфический недостаток — они занимают малую часть окна вывода.

Рис. 11.20. Тор с функциональной окраской поверхности
Задание параметра scaling=unconstrained означает отказ от равного масштаба по осям. График при этом увеличивается в размерах, но становятся заметны его искажения по осям координат. В итоге тор превращается в толстую сплющенную трубу с эллиптическим сечением (рис. 11.21).
Весьма важным является учет углов, под которыми наблюдается трехмерная поверхность или объект. К примеру, построение рис. 11.21 неудачно в том плане, что оно не показывает наличия у тора дырки. В общем, как в поговорке: «кому бублик, а кому дырка от бублика» — ведь бублик и есть материально реализованный тор. Простейший и очень удобный способ изменить угол обзора заключается во вращении фигуры на рисунке мышью при нажатой левой кнопке. При этом можно повернуть фигуру так, что ее геометрические особенности будут видны (рис. 11.22).
В Maple есть способ явно задать углы обзора с помощью параметра orientation=[theta, phi], где theta и phi — углы, через которые задаются параметрические уравнения трехмерной фигуры или поверхности. Рисунок 11.23 дает пример такого задания фигуры, которую можно назвать «квадратным» тором. Обратите внимание, что значения заданных углов обзора повторяются в полях углов на контекстной панели инструментов. Разумеется, последние будут меняться, если начать вращать фигуру на рисунке мышью.

Рис. 11.21. Тор, построенный с применением значения параметра seating-unconstrained

Рис. 11.22. Тор с рис. 11.21 после поворота мышью демонстрирует, что он и впрямь имеет дырку

Рис. 11.23. «Квадратный» тор, представленный под заданными углами обзора
Основная функция построения двумерных графиков plot
В математике широко используются зависимости вида y(x) или у(х). Их графики строятся на плоскости в виде ряда точек y1(x1), обычно соединяемых отрезками прямых. Таким образом, используется кусочно-линейная интерполяция двумерных графиков. Если число точек графика достаточно велико (десятки или сотни), то приближенность построения не очень заметна.
Для построения двумерных графиков служит функция plot. Она задается в виде:
plot(f, h, v)
plot(f, h, v, о)
где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения, v — необязательная переменная с указанием области изменения, о — параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т. д.).
Самыми простыми формами задания этой функции являются следующие:
plot(f ,xrnin,xmax) — построение графика функции f, заданной только своим именем; plot(f(x),x=xmin,xmax) — построение графика функции f(x),Диапазон изменения независимой переменной х задается как xmin. xmax, где xmin и xmax — минимальное и максимальное значение х, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.
Помимо построения самой кривой у(х) или f(x) необходимо задать ряд других свойств графиков, например вывод координатных осей, тип и цвет линий графика и др. Это достигается применением параметров графика — специальных указаний для Maple. Графики обычно (хотя и не всегда) строятся сразу в достаточно приемлемом виде. Это достигается тем, что многие параметры задаются по умолчанию и пользователь, по крайней мере начинающий, может о них ничего не знать. Однако язык общения и программирования Maple 7 позволяет задавать управляющие параметры и в явном виде.
Для двумерного графика возможны следующие параметры:
adaptive — включение адаптивного алгоритма построения графиков (детали см. ниже); axes — вывод различных типов координат (axes=NORMAL — обычные оси, выводятся по умолчанию, axes=BOXES — график заключается в рамку с осями-шкалами, axes=FRAME — оси в виде перекрещенных линий, axes=NONE — оси не выводятся); axes font — задание шрифтов для подписи делений на координатных осях (см.также параметр font); color — задает цвет кривых (см. далее); coords — задание типа координатной системы (см. далее); discont — задает построение непрерывного графика (значения true или false); filled — при filled= true задает окраску цветом, заданным параметром color, для области, ограниченной построенной линией и горизонтальной координатной осью х; font — задание шрифта в виде [семейство, стиль, размер]; labels — задание надписей по координатным осям в виде [X, Y], где X и Y — надписи по осям х и у графика; label directions — задает направление надписей по осям [X, Y], где X и Y может иметь строковые значения HORISONTAL (горизонтально) и VERTICAL (вертикально); label font — задает тип шрифта подписей (см. font); legend — задает вывод легенды (обозначения кривых); linestyle — задание стиля линий (1 — сплошная, 2 — точками, 3 — пунктиром и 4 — штрихпунктиром); numpoints — задает минимальное количество точек на графике (по умолчанию numpoints=49); resolutions — задает горизонтальное разрешение устройства вывода (по умолчанию resolutions=200, параметр используется при отключенном адаптивном методе построения графиков); sample — задает список параметров для предварительного представления кривых; scaling — задает масштаб графика: CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый — по умолчанию); size.— задает размер шрифта в пунктах; style — задает стиль построения графика (POINT — точечный, LINE — линиями); symbol — задает вид символа для точек графика (возможны значения BOX — прямоугольник, CROSS — крест, CIRCLE — окружность, POINT — точка, DIAMOND — ромб); symbol size — установка размеров символов для точек графика (в пунктах, по умолчанию 10); title — задает построение заголовка графика (title="string", где string — строка); titlefont — определяет шрифт для заголовка (см. font); thickness — определяет толщину линий графиков (О, 1, 2, 3, значение по умолчанию — 0); view=[A, В] — определяет максимальные и минимальные координаты, в пределах которых график будет отображаться на экране, А = [xmin. .xmax], B=[ymin. .ymax] (по умолчанию отображается вся кривая); xtickmarks — задает минимальное число отметок по оси x, ytickmarks — задает минимальное число отметок по оси у. В основном задание параметров особых трудностей не вызывает, за исключением задания титульной надписи с выбором шрифтов по умолчанию — в этом случае не всегда поддерживается вывод символов кириллицы (русского языка).
Подбором подходящего шрифта эту проблему удается решить. Модификация графиков с помощью управляющих параметров подробно рассматривается ниже.
Специальный параметр adaptive задает работу специального адаптивного алгоритма для построения графиков наилучшего вида. При этом Maple автоматически учитывает кривизну изменения графика и увеличивает число отрезков прямых в тех частях графиков, где их ход заметно отличается от интерполирующей прямой. При задании adaptive=false адаптивный алгоритм построения графиков отключается, а при adaptive=true включается (значение по умолчанию).
 |
 |
 |
Основные типы двумерных графиков
Графики одной функции
При построении графика одной функции она записывается в явном виде на месте шаблона f. Примеры построения графика одной функции представлены на рис. 11.1. Обратите внимание на то, что график функции sin(x)/x строится без характерного провала в точке х = 0, который наблюдается при построении графиков этой функции многими программами. Он связан с используемым в них правилом — функция задается равной нулю, если ее числитель равен нулю. Данная функция в этой точке дает устранимую неопределенность 0/0->1, что и учитывает графический процессор системы Maple 7.

a

б
Рис. 11.1. Примеры построения графиков одной функции
При построении графиков одной функции могут быть введены описание диапазонов и различные параметры, например: для задания цвета кривой, толщины линии, которой строится график функции, и др. К примеру, запись в списке параметров color=black задает вывод кривых черным цветом, а запись thikness=2 задает во втором примере рис. 11.1 построение графика линией, удвоенной по сравнению с обычной толщиной. Кстати говоря, запись color=red дает красный цвет, color=green — зеленый цвет, color=blue — синий цвет и т. д. При черно-белой печати цвета представляются оттенками серого цвета.
Параметры функции plot3d
Параметры функции plot3d
С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т. д. Следующие параметры функции p1ot3d задаются аналогично их заданию для функции plot:
axesfont font color coords font ,
labelfont linestyle numpoints scaling style
symbol t hickness title titlefont
Однако функция plot3d имеет ряд дополнительных специфических параметров:
ambientl light=[r,g,b] — задает интенсивность красного (r), зеленого (g) и синего (b) цветов подстветки в относительных единицах (от 0 до 1); axes=f — задает вид координатных осей (BOXED, NORMAL, FRAME и NONE, по умолчанию NONE); grid=[m,n] — задает число линий каркаса поверхности; gridstyle=x — задает стиль линий каркаса х ('rectangular' или 'triangular'); 1abels=[x,y,z] — задает надписи по осям (х, у и z — строки, по умолчанию пустые); 1ight=[phi ,theta,r,g,b] — задает углы, под которыми расположен источник освещения поверхности и интенсивности составляющих цвета (г, g и Ь); lightmodel=x — задает схему освещения (соответственно 'none', 'lightl', 'light2', 'lights1 и 'light4'); orientat1on=[theta,phi]— задает углы ориентации поверхности (по умолчанию 45°); projections — задает перспективу при обзоре поверхности (г может быть числом 0 или 1, задающим включение или выключение перспективы, а также одной из строк 'FISHEYE', 'NORMAL' или 'ORTHOGONAL' (это соответствует численным значениям г, равным 0, 0,5 или 1, причем по умолчанию задано projection=ORTHOGONAL)); shading=s — задает направления, по которым меняется цвет функциональной окраски (значения s могут быть XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE); tickmarks=[1 ,n,m] — задает характер маркировки по осямх, у и z (числа 1, n и m имеют значения не менее 1); view=zmin. .zmax или view=[xmin. .xmax, ymin. .ymax, zmin..zmax] — задает минимальные и максимальные координаты поверхности для ее видимых участков.
Построение фигур в различных системах координат
Построение фигур в различных системах координат
Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рисунок 11.16 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.
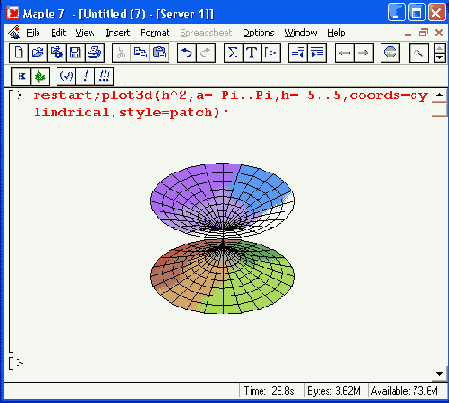
При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи (кстати, сделанной на русском языке).
Приведем еще один пример построения трехмерной поверхности — на этот раз . в сферической системе координат (рис. 11.17). Здесь функция задана вообще элементарно просто — в виде числа 1. Но, поскольку выбрана сферическая система координат, в результате строится поверхность шара единичного радиуса.
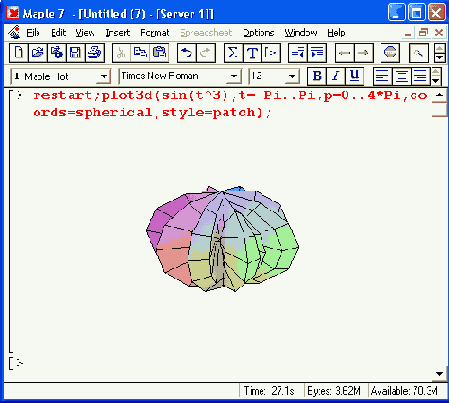
О том, насколько необычным может быть график той или иной функции в различных системах координат, свидетельствует рис. 11.18. На нем показан график параметрически заданной функции от одной координаты t = sin(t3), построенный в сферической системе координат.
Кстати, рис. 11.18 иллюстрирует возможность одновременного наблюдения нескольких окон. В одном окне задано построение графика, а в другом построен сам график. При построении графика в отдельном окне появляется панель форматирования графика. С помощью ее довольно наглядных кнопок можно легко скорректировать вспомогательные параметры графика (окраску, наличие линий каркаса, ориентацию и др.).

 |
 |
 |
Построение поверхностей
Построение поверхностей с разными стилями
На рис. 11.15 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию в Maple 7 строится поверхность с функциональной окраской и стилем style=patch (верхний рисунок). Функциональная окраска делает рисунки более информативными, но, увы, на рисунках в книге она превращается в окраску оттенками серого цвета.
Параметр style=hidden строит каркасную поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение во втором примере задано линиями/черного цвета с помощью параметра color=black (см. нижний рисунок на рис. (11.15).
Помимо значения patch для построения трехмерных поверхностей можно задавать ряд других стилей: point — точками, contour — контурными линиями, line — линиями, hidden — линиями каркаса с удалением невидимых линий, wireframe — линиями каркаса со всеми видимыми линиями, patchnogrid — с раскраской, но без линий каркаса, patchcontour — раскраска с линиями равного уровня.

а

б
Рис. 11.15. Примеры простейшего построения трехмерных поверхностей
Цвет трехмерного графика может задаваться (как и для двумерного) параметром соlог=с, где с — цвет (оттенки цвета перечислялись ранее). Возможно еще два алгоритма задания цвета:
HUE — алгоритм с заданием цвета в виде color=f(x,y); RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения ехрrr, ехрrg и exprb задают относительную значимость (от 0 до 1) основных цветов (красного — ехрrr, зеленого — ехрrg и синего — exprb).Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.
Построение ряда трехмерных фигур на одном графике
Построение ряда трехмерных фигур на одном графике
Функция plot3d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. Для этого достаточно вместо описания одной поверхности задать список описаний ряда поверхностей. При этом функция plot3d обладает уникальной возможностью — автоматически вычисляет точки пересечения фигур и показывает только видимые части поверхностей. Это создает изображения, выглядящие вполне естественно. Пример такого построения для двух функций показан на рис. 11.30.

 |
 |
 |
Построение трехмерных графиков
Особенности применения функции plot3d
Трехмерными называют графики, отображающие функции двух переменных z(х,у). Каждая точка zi таких графиков является высотой (аппликатой) точки, лежащей в плоскости XY и представленной координатами (х,у). Поскольку экран монитора компьютера в первом приближении является плоским, то на деле трехмерные графики представляют собой специальные проекции объемных объектов.

а

б
Рис. 11.14. Построение графиков функций в полярной системе координат
Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию pi ot3d. Она может использоваться в следующих форматах:
plot3d(exprl. x=a..b. y=c..d,p)
plot3d(f, a..b. c..d.p)
plot3d([exprf.exprg.exprh]. s=a..b, t=c..d.p)
plot3d([f.g.h]. a..b, c..d,p)
В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах записи f, g и h — функции; exprl — выражение, отражающее зависимость от -х и у; exprf, exprg и exprh — выражения, задающие поверхность параметрически; s, t, а и b — числовые константы действительного типа; end — числовые константы или выражения действительного типа; х, у, s и t — имена независимых переменных; р — управляющие параметры.
Специальные приемы построения трехмерных графиков
Трехмерный график как графический объект
Принадлежность функций plot и plot3d к функциям (в ряде книг их именуют операторами, командами или процедурами) наглядно выявляется при создании графических объектов. Графический объект — это, в сущности, обычная переменная, которой присваивается значение графической функции. После этого такая переменная, будучи вызванной, производит построение соответствующего графика. Пример этого дан на рис. 11.28.
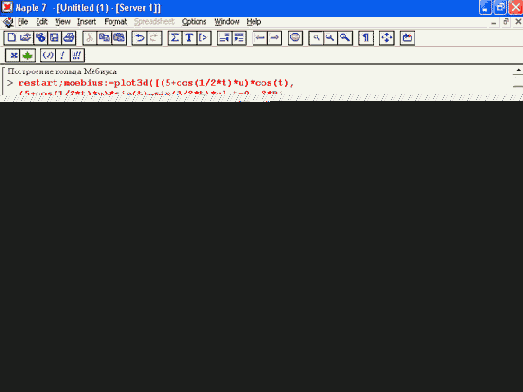
Рис. 11.28. Пример задания и вывода трехмерного графика — графического объекта
В данном случае строится лента Мебиуса, свойства которой (например, плавный переход с одной стороны ленты на другую) уже много веков будоражат воображение людей.
Поскольку можно говорить, что вызов переменной возвращает графический объект, то это дает повод считать plot и plot3d графическими функциями.
Управление диапазоном изменения переменной и значения функции
Для управления отображаемой на графике области служит задание диапазонов принимаемых значений для переменной и функции. В ряде случаев их можно не применять, тогда Maple автоматически задает приемлемые диапазоны. Однако их явное указание позволяет управлять областью графика вручную. Иногда соответствующее задание диапазонов случайно или целенаправленно ведет к отсечению части графика — например, на рис. 11.2 в первом примере отсечена верхняя часть графика.

а

б
Рис. 11.2. Построение графиков функции с явным указанием масштаба
Правильный выбор диапазонов повышает представительность графиков функций. Рекомендуется вначале пробовать строить графики с автоматическим выбором диапазонов, а уже затем указывать их вручную.
Управление стилем и цветом линий двумерных графиков
Maple 7 позволяет воспроизводить на одном графике множество кривых. При этом возникает необходимость как-то идентифицировать их. Для этого можно использовать построение линий разными стилями, разными цветами и с разной толщиной. Набор средств выделения кривых позволяет уверенно различать их как на экране цветного дисплея и в распечатках, сделанных цветным струйным принтером, так и при печати монохромными принтерами. Параметр style — позволяет задавать следующие стили для линий графиков:
POINT или point — график выводится по точкам; LINE или line — график выводится линией.Если задано построение графика точками, то параметр symbol позволяет представить точки в виде различных символов, например прямоугольников, крестов, окружностей или ромбов.
Другой параметр — color — позволяет использовать обширный набор цветов линий графиков:
| aquamarine |
black |
blue |
navy |
coral |
|
| cyan |
brown |
gold |
green |
gray |
|
| grey |
khaki |
magenta |
maroon |
orange |
|
| pink |
plum |
red |
sienna |
tan |
|
| turquoise |
violet |
wheat |
white |
yellow |
Различные цветовые оттенки получаются благодаря использованию RGB-комбинаций базовых цветов: red — красный, gray — зеленый, bluе — синий. Приведем перевод ряда других составных цветов: black — черный, white — белый, khaki — цвет «хаки», gold — золотистый, orange — оранжевый, violet — фиолетовый, yellow — желтый и т. д. Перевод цветов некоторых оттенков на русский язык не всегда однозначен и потому не приводится. Средства управления стилем графиков дают возможность легко выделять различные кривые на одном рисунке, даже если для выделения не используются цвета.
 |
 |
 |
Введение в построение двумерных графиков
Основные возможности двумерной графики
Maple 7 реализует все мыслимые (и даже «немыслимые») варианты математических графиков. Строятся как графики простых функций в декартовой и полярной системах координат, так и графики, показывающие реалистические образы сложных, пересекающихся в пространстве фигур с их функциональной окраской. Возможны наглядные графические иллюстрации решений самых разнообразных уравнений, включая системы дифференциальных уравнений.
В само ядро Maple 7 встроено ограниченное число функций построения графиков. Это прежде всего функция для построения двумерных графиков plot и функция для построения трехмерных графиков plotSd. Они позволяют строить графики наиболее распространенных типов. Для построения специальных графиков (например, векторных полей градиентов, решения дифференциальных уравнений, построения фазовых портретов и т. д.) в пакеты системы Maple 7 включено большое число различных графических функций. Для их вызова необходимы соответствующие указания.
Вообще говоря, средства для построения графиков в большинстве языков программирования принято считать графическими процедурами, или операторами. Однако мы сохраним за ними наименование функций, в силу двух принципиально важных свойств:
О графические средства Maple V возвращают некоторые графические объекты, которые размещаются в окне документа — в строке вывода или в отдельном графическом объекте;
О эти объекты можно использовать в качестве значений переменных, то есть переменным можно присваивать значения графических объектов и выполнять над ними соответствующие операции (например, с помощью функции show выводить на экран несколько графиков).
Графические функции заданы таким образом, что обеспечивают построение типовых графиков без какой-либо особой подготовки. Для этого нужно лишь указать функцию, график которой строится, и пределы изменения независимых переменных. Однако с помощью дополнительных необязательных параметров можно существенно изменить вид графиков — например, настроить стиль и цвет линий, вывести титульную надпись, изменить вид координатных осей и т. д.
 |
 |
Выбор и пересчет координат трехмерных графиков
Выбор и пересчет координат трехмерных графиков
Для трехмерных графиков возможно задание 31 типа координатных систем с помощью параметра сооrds= Тип _ координатной _ системы. Поскольку на экране монитора поверхность отображается только в прямоугольной системе координат и характеризуется координатами х, у и z, то для представления поверхности, заданной в иной системе координат с координатами u, v и w, используются известные [46, 47] формулы для преобразования (u, v, w) --> (х, у, z). Ниже перечислены типы трехмерных координатных систем и соответствующие формулы преобразования.
bipolar-cylindrical:
х = a*sinh(v)/(cosh(v)-cos'(u))
у = a*sin(u)/(cosh(v)-cos(u))
z = w
bispherical:
x = sin(u)*cos(w)/d
у = sin(u)*sin(w)/d
z = sinh(v)/d где d - cosh(v) - cos(u)
cardioidal:
x = u*v*cos(w)/(u^2+v^2)^2
у -=u*v*sin(w)/(u^2+v^2)^2
z = (u^2-v^2)/2/(u^2+v^2)^2
cardioidcylindrical:
x = (u^2-v^2)/2/(u^2+v^2)^2
у - u*v/(u^2+v^2)^2
z =w
casscylindhcal:
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2)+exp(u)*cos(v)+l)^(l/2)
у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2)-exp(u)*cos(v)-l)^(l/2)
z =w
confocalellip:
x = ((a^2-u)*(a^2-v)*(a^2-w)/(a^2-b^2)/(a^2-c^2))^(l/2)
у = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2)/(b^2-c^2))^(l/2)
z = ((c^2-u)*(c^2-v)*(c^2-w)/(c^2-a^2)/(c^2-b^2))^(l/2)
confocalparab:
x = ((a^2-u)*(a^2-v)*(a^2-w)/(b^2-a^2)^(l/2)
у = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2))^(l/2)
z = (a^2+b^2-u-v-w)/2
conical:
x = u*v*w/(a*b)
у = u/b*((v^2 - b^2)*(b^2-w^2)/(a^2-b^2))^(l/2)
z= u/a*((a^2 - v^2)*(a^2 - w^2)/(a^2-b^2))6(l/2)
cylindrical:
x = u*cos(y)
у = u*sin(y)
z = w
ellcylindrical:
x =a*cosh(u)*cos(v)
у = a*sinh(u)*sin(v)
z = w
ellipsoidal:
x = u*v*w/a/b
у = ((u^2-b^2)*(u^2-b^2)*(b^2-w^2)/(а^2-b^2)^(1/2)/b
z = ((u^2-a^2)*(a^2-v^2)*(a^2-w^2)/(a^2-b^2)^(l/2)/a
hypercylindrical:
x = ((u^2+v^2)^(l/2)-ni)^(l/2)
у = ((u^2+v^2)^(l/2)-u)^(l/2)
z = w
invcasscylindrical:
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) +
exp(u)*cos(v)+1)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(l/2)
у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(l/2) -
exp(u)*cos(v)-1)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)-1)^(l/2)
z = w
invellcylindrical:
x = a*cosh(u)*cos(v)/(cosh(u)^2-sin(v)^2)
у = a*sinh(u)*sin(v)/(cosh(u)^2-sin(v)^2)
z = w
invoblspheroidal:
x = a*cosh(u)*sin(v)*cos(w)/(cosh(u)^2-cos(v)^2)
у = a*cosh(u)*sin(v)*sin(w)/(cosh(u)^2-cos(v)^2)
z = a*sinh(u)*cos(v)/(cosh(u)^2-cos(v)^2)
invprospheroldal:
x = a*s1nh(u)*sin(v)*cos(w)/(cosh(u)^2-sin(v)^2)
у = a*sinh(u)*sin(v)*sin(w)/(cosh(u)^2-sin(v)^2)
z = a*cosh(u)*cos(v)/(cosh(u)^2-s1n(v)^2)
logcyllndrical:
x = a/Pi*ln(u^2+v^2)
у = 2*a/Pi*arctan(v/u)
z = w
logcoshcylindrical:
x = a/Pi*ln(cosh(u^2-sin(v)^2)
у = 2*a/Pi*arctan(tanh(u)*tan(v))
z = w
maxwell cylindrical:
x = a/P1*(u+l+exp(u)*cos(v))
у = a/Pi*(v+exp(u)*sin(v))
z = w
oblatespheroidal:
x = a*cosh(u)*s1n(v)*cos(w)
у = a*cosh(u)*sin(v)*sin(w)
z = a*s1nh(u)*cos(v)
parabololdal:
x = u*v*cos(w)
у = u*v*sin(w)
z = (u^2 - v^2)/2
paraboloidal2:
x = 2*((u-a)*(a-v)*(a-w)/(a-b)^(l/2)
у = 2*((u-b)*(b-v)*(b-w)/(a-b))^(l/2)
z = u+v+w-a-b
paracylindrical:
x = (iT2 - v*2)/2
у =u*v
z = w
prolatespheroidal:
x = a*sinh(u)*sin(v)*cos(w)
y=a*s1nh(u)*sin(v)*sin(w)
z=a*cosh(u)*cos(v)
rectangular:
x = u
у = v
z = w
rosecylindrlcal:
х =((u^2+v^2)^(l/2)-Hi)^(l/2)/(u^2+v^2)^(l/2)
у = ((u^2+v^2)^(l/2)-u)^(l/2)/(u^2+v^2)^(l/2)
z =w
sixsphere:
x = u/(u^2+v^2+w^2)
у = v/(u^2+v^2+w^2)
z = w/(u^2+v^2+w^2)
spherical:
x = u*cos(v)*sin(w)
у = u*sin(v)*sin(w)
z = u*cos(w)
tangentcylindrical:
x = u/(u^2+v^2) '
у = v/(u^2+v^2)
z = w
tangentsphere:
x = u*cos(w)/(u^2+v^2)
у = u*sin(w)/(u^2+v^2)
z = v/(u^2+v^2)
toroidal:
x = a*sinh(v)*cos(w)/d
у = a*sinh(v)*sin(w)/d
z = a*sin(u)/d где d = cosh(v) - cos(u)
Эти формулы полезно знать, поскольку в литературе встречаются несколько отличные формулы пересчета. Вид графиков трехмерных поверхностей очень сильно различается в разных координатных системах. По умолчанию трехмерные графики строятся в прямоугольной системе координат — rectangular.
 |
 |
 |
Задание координатных систем двумерных графиков
Задание координатных систем двумерных графиков
В версии Maple 7 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию используется прямоугольная (декартова) система координат (coords=cartesian). При использовании других координатных систем координаты точек для них(и, v) преобразуются в координаты (х, у) как (n, v) —> (х, у). Ниже приведены наименования систем координат (значений параметра coords) и соответствующие формулы преобразования.
| bipolar: |
x = sinh(v)/(cosh(v)-cos(u)) у - sin(u)/(cosh(v)-cos(u)) |
| cardioid: |
x = l/2*(u^2-v^2)/(u^2+v^2)^2 у = u*v/(u^2+v^2)^2 |
| cartesian: |
x = u У = v |
| cassinian: |
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) + exp(u)*cos(v)+1^(l/2) у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) -exp(u)*cos(v)-1)^(l/2)] |
| elliptic: |
x = cosh(u)*cos(v) у = sinh(u)*sin(v) |
| hyperbolic: |
x = ((u^2+v^2)^(l/2)+u)^(l/2) у = ((u^2+v~2)^(l/2)-u)^(l/2) |
| invcassinian: |
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) + exp(u)*cos(v)+1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(l/2) у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) -exp(u)*cos(v)-l)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) |
| invelliptic: |
x = a*cosh(u)*cos(v)/(cosh(u)*2-sin(v)*2) у = a*sinh(u)*sin(v)/(cosh(u)^2-sin(vr2) |
| logarithmic: |
x = a/Pi*ln(u^2+v^2) у = 2*a/Pi*arctan(v/u) |
| logcosh: |
x = a/Pi*ln(cosh(ur2-sin(vr2) у =2*a/Pi*arctan(tanh(u)*tan(v)) |
| maxwell : |
x - a/Pi*(u+l+exp(u)*cos(v)) у = a/Pi*(v+exp(u)*sin(v)) |
| parabolic: |
x = (u^2-v^2)/2 • у - u*v |
| polar: |
x = u*cos(v) у = u*sin(v) |
| rose: |
x = ((u^2+v^2)^(l/2)+u)^(l/2)/(u^2+v^2)^(l/2) у - ((u^2+v^(1/2)+u)^(1/2)/(u^2+v^2)^(1/2) |
| tangent: |
x = u/(u^2+v^2) у =v/(u^2+v^2) |
 |
 |
 |
Задание трехмерных графиков в виде процедур
в процедурах любых внутренних функций,
Задание трехмерных графиков в виде процедур
Язык программирования Maple 7 допускает применение в процедурах любых внутренних функций, в том числе графических. Пример такого применения дает рис. 11.29.

Этот пример показывает еще один способ задания и построения кольца Мебиуса. Практически любые графические построения можно оформлять в виде процедур и использовать такие процедуры в своих документах.
Занимательные фигуры — трехмерные графики
Параметрическое задание уравнений поверхности открывает почти неисчерпаемые возможности построения занимательных и сложных фигур самого различного вида. Приведем пару построений такого рода.
На рис. 11.24 показан тор, сечение которого имеет вид сплюснутой шестиконечной звезды. Вырез в фигуре дает прекрасный обзор ее внутренней поверхности, а цветная функциональная окраска и линии сетки, построенные с применением алгоритма удаления невидимых линий, дают весьма реалистичный вид фигуры. Замените параметр scaling=unconstrained на scaling=constrained, и вы получите тор с неискаженным сечением.
На рис. 11.25 показан еще один тор. На этот раз он круглого сечения, но сверху и снизу имеет вид пятиконечной звезды.
ПРИМЕЧАНИЕ
В приведенных на рис. 11.19-11.25 программах построения различных поверхностей — и трехмерных фигур имеется ряд характерных констант и математических выражений, определяющих как вид фигур, так и их размеры и положение. Рекомендуется тщательно проанализировать эти примеры и попробовать их в работе с несколько измененными теми или иными данными. Полезно построить ряд подобных примеров самостоятельно. Все это будет способствовать привитию учащимся специального геометрического стиля мышления, при котором геометрические особенности фигур связываются с их расчетным описанием.

Рис. 11.24. Тор с сечением в виде шестиконечной звезды
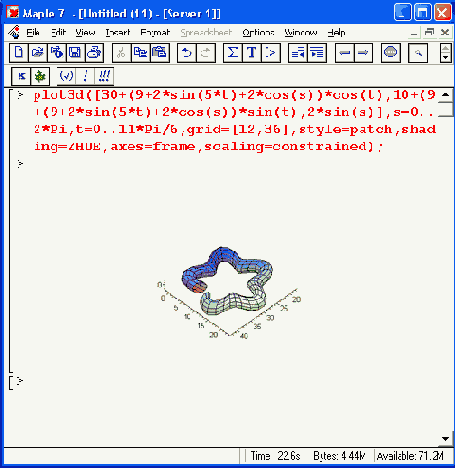
Рис. 11.25. Тор круглого сечения в виде пятиконечной звезды