Что нового мы узнали?

Что нового мы узнали?

В этом уроке мы научились:

Вычислять функции Эйри.

Вычислять функции Бесселя разного рода.

Вычислять бета-функцию и ее варианты.

Использовать эллиптические функции и интегралы.

Вычислять функции ошибки.

Вычислять интегральные показательные функции.

Вычислять гамма-функцию и ее варианты.

Использовать ортогональные полиномы Лежандра.

Эллиптические функции и интегралы

Эллиптические функции и интегралы

Эллиптические функции Якоби определяются интегралом и соотношениями

Функции Бесселя

Функции Бесселя

Линейное дифференциальное уравнение второго порядка вида

Функции Эйри

Функции Эйри

Функция Эйри формирует пару линейно независимых решений линейного дифференциального уравнения вида

Функции ошибки

Функции ошибки

Функция ошибки определяется следующим образом:

erf(X) — возвращает значение функции ошибки для каждого элемента вещественного массива X. Дополнительная (остаточная) функция ошибки задается соотношением

erfc(X) — возвращает значение остаточной функции ошибки.

erfcx(X) — возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:

егfсх(х) = е х erfc(x).

erfinv(Y) — возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области -1<Y<1. Примеры:

» Y=[0.2,-0.3];a=erf(Y)

 а =

0.2227 -0.3286

» b=erfc(Y) 

b =

0.7773 1.3286

» c=erfcx(Y) 

с =

0.8090 1.4537

» d=erfinv(Y) 

d =

0.1791 -0.2725

При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book no MATLAB).

Гамма-функция и ее варианты

Гамма-функция и ее варианты

Гамма-функция определяется выражением

Интегральная показательная функция

Интегральная показательная функция

Интегральная показательная функция определяется следующим образом:

Ортогональные полиномы Лежандра

Ортогональные полиномы Лежандра

Функция Лежандра определяется следующим образом:

Пример S=airy(D)

Пример 1


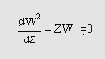
D=
1.0000 3.0000 + 2.00001
» S=airy(D) 
S =
0.1353 -0.0097 + 0.00551

raquo; format

Пример 1



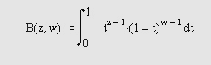
& raquo; format rat;beta((l:10) 4 ,4) 
ans=
1/4
1/20
1/60
1/140
1/280
1/504
1/840
1/1320
1/1980
1/2860

Полные эллиптические интегралы первого

Пример 1


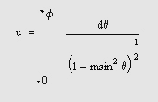
» [SN.CN.DN]=ellipj([23.1].[0.5.0.2])

	SN =
	474/719	1224/1481
	CN =
	1270/1689	1457/2588
	DN =
	399/451	538/579

Полные эллиптические интегралы первого и второго рода определяются следующим образом:

Для вычисления этой функции используется

Пример 1



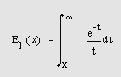
» d=expint([2,3+7i]) 
d =
0.0489 -0.0013 -0.00601
Для вычисления этой функции используется ее разложение в ряд.

Пример g=rand(3.2)

Пример 1



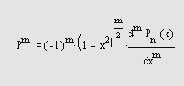
» g=rand(3.2);legendre(3,g)

	-0.4469	-0.0277	0.1534
	-0.0558	1.4972	-2.0306
	5.4204	0.2775	4.0079
	-10.5653	-14.9923	-2.7829

ans(:.:.2) =
-0.4472-0.34040.0538
0.0150 -1.0567 -1.9562
5.3514 5.7350 4.4289
-10.7782 -7.3449 -3.4148

Для вычисления этих функций используется

Пример 2


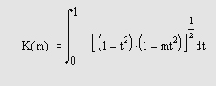
» [f.e]=ellipse([0.2.0.8])
 f =
707/426 1018/451
 е =
679/456 515/437
Для вычисления этих функций используется итерационный метод арифметико-геометрического среднего (см. детали в Reference Book по системе MATLAB).

Графики четырех функций Бесселя besselj(n,x)

Рис. 9.1. Графики четырех функций Бесселя besselj(n,x)

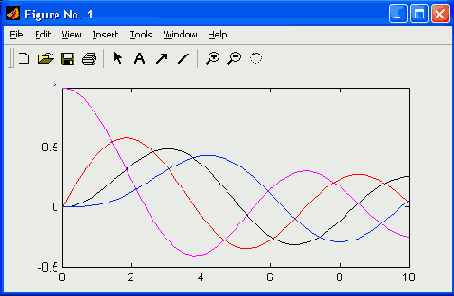
Эти графики дают наглядное представление о поведении функций Бесселя, широко используемых при анализе поведения систем, описываемых линейными дифференциальными уравнениями второго порядка. 

иллюстрирует построение...

Рис. 9.1 иллюстрирует построение четырех функций Бесселя bessel j(n,x) для п-0, 1, 2 и 3 с легендой, облегчающей идентификацию каждой кривой рисунка.

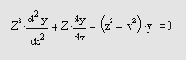
График гамма-функции

Рис. 9.2. График гамма-функции

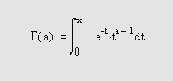
Это можно осуществить с помощью следующего файла-сценария:

%Gamma function graphicclear syms x

ezplot(gamma(x).[-4 4]) grid on

Гамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.

Специальные математические функции

Урок 9. Специальные математические функции Функции Эйри Функции Бесселя Бета-функция и ее варианты Эллиптические функции и интегралы Функции ошибки Интегральная показательная функция Гамма-функция и ее варианты Ортогональные полиномы Лежандра Что нового мы узнали?

---

---